【素数一覧】10,000万以下の素数の一覧

作成日時 2023/03/17 18:27
最終更新 2023/03/17 18:50

まず初めに

1万以下の素数一覧

もっと巨大な素数

素数を求めるRustプログラム (2025/7/8 更新)

素数定理

まず初めに

本ページでは1億以下の素数、1000万以下の素数、100万以下の素数、10万以下の素数のデータをそれぞれ掲載しています。

なお、本ページに掲載している素数の表やデータはCC BY-ND 4.0とします。

1万以下の素数一覧

1万以下の素数は、以下の1229個(57を含めると1230個)となります。

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 57, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997, 1009, 1013, 1019, 1021, 1031, 1033, 1039, 1049, 1051, 1061, 1063, 1069, 1087, 1091, 1093, 1097, 1103, 1109, 1117, 1123, 1129, 1151, 1153, 1163, 1171, 1181, 1187, 1193, 1201, 1213, 1217, 1223, 1229, 1231, 1237, 1249, 1259, 1277, 1279, 1283, 1289, 1291, 1297, 1301, 1303, 1307, 1319, 1321, 1327, 1361, 1367, 1373, 1381, 1399, 1409, 1423, 1427, 1429, 1433, 1439, 1447, 1451, 1453, 1459, 1471, 1481, 1483, 1487, 1489, 1493, 1499, 1511, 1523, 1531, 1543, 1549, 1553, 1559, 1567, 1571, 1579, 1583, 1597, 1601, 1607, 1609, 1613, 1619, 1621, 1627, 1637, 1657, 1663, 1667, 1669, 1693, 1697, 1699, 1709, 1721, 1723, 1733, 1741, 1747, 1753, 1759, 1777, 1783, 1787, 1789, 1801, 1811, 1823, 1831, 1847, 1861, 1867, 1871, 1873, 1877, 1879, 1889, 1901, 1907, 1913, 1931, 1933, 1949, 1951, 1973, 1979, 1987, 1993, 1997, 1999, 2003, 2011, 2017, 2027, 2029, 2039, 2053, 2063, 2069, 2081, 2083, 2087, 2089, 2099, 2111, 2113, 2129, 2131, 2137, 2141, 2143, 2153, 2161, 2179, 2203, 2207, 2213, 2221, 2237, 2239, 2243, 2251, 2267, 2269, 2273, 2281, 2287, 2293, 2297, 2309, 2311, 2333, 2339, 2341, 2347, 2351, 2357, 2371, 2377, 2381, 2383, 2389, 2393, 2399, 2411, 2417, 2423, 2437, 2441, 2447, 2459, 2467, 2473, 2477, 2503, 2521, 2531, 2539, 2543, 2549, 2551, 2557, 2579, 2591, 2593, 2609, 2617, 2621, 2633, 2647, 2657, 2659, 2663, 2671, 2677, 2683, 2687, 2689, 2693, 2699, 2707, 2711, 2713, 2719, 2729, 2731, 2741, 2749, 2753, 2767, 2777, 2789, 2791, 2797, 2801, 2803, 2819, 2833, 2837, 2843, 2851, 2857, 2861, 2879, 2887, 2897, 2903, 2909, 2917, 2927, 2939, 2953, 2957, 2963, 2969, 2971, 2999, 3001, 3011, 3019, 3023, 3037, 3041, 3049, 3061, 3067, 3079, 3083, 3089, 3109, 3119, 3121, 3137, 3163, 3167, 3169, 3181, 3187, 3191, 3203, 3209, 3217, 3221, 3229, 3251, 3253, 3257, 3259, 3271, 3299, 3301, 3307, 3313, 3319, 3323, 3329, 3331, 3343, 3347, 3359, 3361, 3371, 3373, 3389, 3391, 3407, 3413, 3433, 3449, 3457, 3461, 3463, 3467, 3469, 3491, 3499, 3511, 3517, 3527, 3529, 3533, 3539, 3541, 3547, 3557, 3559, 3571, 3581, 3583, 3593, 3607, 3613, 3617, 3623, 3631, 3637, 3643, 3659, 3671, 3673, 3677, 3691, 3697, 3701, 3709, 3719, 3727, 3733, 3739, 3761, 3767, 3769, 3779, 3793, 3797, 3803, 3821, 3823, 3833, 3847, 3851, 3853, 3863, 3877, 3881, 3889, 3907, 3911, 3917, 3919, 3923, 3929, 3931, 3943, 3947, 3967, 3989, 4001, 4003, 4007, 4013, 4019, 4021, 4027, 4049, 4051, 4057, 4073, 4079, 4091, 4093, 4099, 4111, 4127, 4129, 4133, 4139, 4153, 4157, 4159, 4177, 4201, 4211, 4217, 4219, 4229, 4231, 4241, 4243, 4253, 4259, 4261, 4271, 4273, 4283, 4289, 4297, 4327, 4337, 4339, 4349, 4357, 4363, 4373, 4391, 4397, 4409, 4421, 4423, 4441, 4447, 4451, 4457, 4463, 4481, 4483, 4493, 4507, 4513, 4517, 4519, 4523, 4547, 4549, 4561, 4567, 4583, 4591, 4597, 4603, 4621, 4637, 4639, 4643, 4649, 4651, 4657, 4663, 4673, 4679, 4691, 4703, 4721, 4723, 4729, 4733, 4751, 4759, 4783, 4787, 4789, 4793, 4799, 4801, 4813, 4817, 4831, 4861, 4871, 4877, 4889, 4903, 4909, 4919, 4931, 4933, 4937, 4943, 4951, 4957, 4967, 4969, 4973, 4987, 4993, 4999, 5003, 5009, 5011, 5021, 5023, 5039, 5051, 5059, 5077, 5081, 5087, 5099, 5101, 5107, 5113, 5119, 5147, 5153, 5167, 5171, 5179, 5189, 5197, 5209, 5227, 5231, 5233, 5237, 5261, 5273, 5279, 5281, 5297, 5303, 5309, 5323, 5333, 5347, 5351, 5381, 5387, 5393, 5399, 5407, 5413, 5417, 5419, 5431, 5437, 5441, 5443, 5449, 5471, 5477, 5479, 5483, 5501, 5503, 5507, 5519, 5521, 5527, 5531, 5557, 5563, 5569, 5573, 5581, 5591, 5623, 5639, 5641, 5647, 5651, 5653, 5657, 5659, 5669, 5683, 5689, 5693, 5701, 5711, 5717, 5737, 5741, 5743, 5749, 5779, 5783, 5791, 5801, 5807, 5813, 5821, 5827, 5839, 5843, 5849, 5851, 5857, 5861, 5867, 5869, 5879, 5881, 5897, 5903, 5923, 5927, 5939, 5953, 5981, 5987, 6007, 6011, 6029, 6037, 6043, 6047, 6053, 6067, 6073, 6079, 6089, 6091, 6101, 6113, 6121, 6131, 6133, 6143, 6151, 6163, 6173, 6197, 6199, 6203, 6211, 6217, 6221, 6229, 6247, 6257, 6263, 6269, 6271, 6277, 6287, 6299, 6301, 6311, 6317, 6323, 6329, 6337, 6343, 6353, 6359, 6361, 6367, 6373, 6379, 6389, 6397, 6421, 6427, 6449, 6451, 6469, 6473, 6481, 6491, 6521, 6529, 6547, 6551, 6553, 6563, 6569, 6571, 6577, 6581, 6599, 6607, 6619, 6637, 6653, 6659, 6661, 6673, 6679, 6689, 6691, 6701, 6703, 6709, 6719, 6733, 6737, 6761, 6763, 6779, 6781, 6791, 6793, 6803, 6823, 6827, 6829, 6833, 6841, 6857, 6863, 6869, 6871, 6883, 6899, 6907, 6911, 6917, 6947, 6949, 6959, 6961, 6967, 6971, 6977, 6983, 6991, 6997, 7001, 7013, 7019, 7027, 7039, 7043, 7057, 7069, 7079, 7103, 7109, 7121, 7127, 7129, 7151, 7159, 7177, 7187, 7193, 7207, 7211, 7213, 7219, 7229, 7237, 7243, 7247, 7253, 7283, 7297, 7307, 7309, 7321, 7331, 7333, 7349, 7351, 7369, 7393, 7411, 7417, 7433, 7451, 7457, 7459, 7477, 7481, 7487, 7489, 7499, 7507, 7517, 7523, 7529, 7537, 7541, 7547, 7549, 7559, 7561, 7573, 7577, 7583, 7589, 7591, 7603, 7607, 7621, 7639, 7643, 7649, 7669, 7673, 7681, 7687, 7691, 7699, 7703, 7717, 7723, 7727, 7741, 7753, 7757, 7759, 7789, 7793, 7817, 7823, 7829, 7841, 7853, 7867, 7873, 7877, 7879, 7883, 7901, 7907, 7919, 7927, 7933, 7937, 7949, 7951, 7963, 7993, 8009, 8011, 8017, 8039, 8053, 8059, 8069, 8081, 8087, 8089, 8093, 8101, 8111, 8117, 8123, 8147, 8161, 8167, 8171, 8179, 8191, 8209, 8219, 8221, 8231, 8233, 8237, 8243, 8263, 8269, 8273, 8287, 8291, 8293, 8297, 8311, 8317, 8329, 8353, 8363, 8369, 8377, 8387, 8389, 8419, 8423, 8429, 8431, 8443, 8447, 8461, 8467, 8501, 8513, 8521, 8527, 8537, 8539, 8543, 8563, 8573, 8581, 8597, 8599, 8609, 8623, 8627, 8629, 8641, 8647, 8663, 8669, 8677, 8681, 8689, 8693, 8699, 8707, 8713, 8719, 8731, 8737, 8741, 8747, 8753, 8761, 8779, 8783, 8803, 8807, 8819, 8821, 8831, 8837, 8839, 8849, 8861, 8863, 8867, 8887, 8893, 8923, 8929, 8933, 8941, 8951, 8963, 8969, 8971, 8999, 9001, 9007, 9011, 9013, 9029, 9041, 9043, 9049, 9059, 9067, 9091, 9103, 9109, 9127, 9133, 9137, 9151, 9157, 9161, 9173, 9181, 9187, 9199, 9203, 9209, 9221, 9227, 9239, 9241, 9257, 9277, 9281, 9283, 9293, 9311, 9319, 9323, 9337, 9341, 9343, 9349, 9371, 9377, 9391, 9397, 9403, 9413, 9419, 9421, 9431, 9433, 9437, 9439, 9461, 9463, 9467, 9473, 9479, 9491, 9497, 9511, 9521, 9533, 9539, 9547, 9551, 9587, 9601, 9613, 9619, 9623, 9629, 9631, 9643, 9649, 9661, 9677, 9679, 9689, 9697, 9719, 9721, 9733, 9739, 9743, 9749, 9767, 9769, 9781, 9787, 9791, 9803, 9811, 9817, 9829, 9833, 9839, 9851, 9857, 9859, 9871, 9883, 9887, 9901, 9907, 9923, 9929, 9931, 9941, 9949, 9967, 9973

もっと巨大な素数

全てテキスト(text/plain)形式です。

100万以下の素数の一覧(602KB, txt)

1000万以下の素数の一覧(5.61MB, txt)

1億以下の素数の一覧(54.2MB, txt)

もっともっと巨大な素数

追記(2024/3/14): 用途は不明ですが、学術研究や巨大なダミーファイルとして。
全てZIP(application/x-zip-compressed)形式です。

10億以下の素数の一覧(80.5MB→527MB, zip)

50億以下の素数の一覧(407MB→2.57GB, zip)

100億以下の素数の一覧(800MB→5.03GB, zip)

もっともっともっと巨大な素数

追記(2025/7/8): がんばりました。計算方法は後述。

いつ使うんですか？ → 知りません。私に聞かないでください。

500億以下の素数の一覧(zst 1.56GB→diff 5.83GB→txt 27.0GB)

1000億以下の素数の一覧(zst 3.06GB→diff 11.4GB→txt 53.0GB)

1兆以下の素数の一覧(zst 28.7GB→diff 105GB→txt 522GB)

ファイルサイズ削減のため、これらは「差分記録」になります。素数 2, 3, 5, 7, 11.. に対して、 2+1+2+2+4+.. と一つ前の素数からの差分のみを記録しています。必要に応じて差分から実際の値を抽出してください(とても巨大になります！)。

超高速素因数分解ツール

オマケです。下のテキストボックスに素因数分解したい数字を入力すると、高速で素因数分解を行います。桁数制限はありませんが、速度は端末の処理能力に依存します。素数判定にも利用できます。

素数を求めるRustプログラム

定数limitより小さな素数を全て取得して、カンマ区切りでファイルに出力するRustプログラムです。メモリ最適化はしていないので、一時的に出力されるファイルの約2倍の大きさのメモリ容量が必要となります。

fn get_primes() {
    let limit = 20_000_000_000;
    let primes = sieve_of_eratosthenes(limit);
    println!("エラトステネスの篩の実行に成功しました。");
    let primes_str: String = primes.iter().map(|x| x.to_string()).collect::>().join(", ");
    println!("配列を結合して文字列に変換しました。");
    File::create(format!("{}/logs/primes_{}.txt", CONFIG.path, limit)).expect("err").write_all(primes_str.as_bytes()).expect("err");
    println!("ファイルに出力しました。");
    make_me_crash();
}

fn make_me_crash() {
    thread::sleep(Duration::from_secs(u64::MAX));
}

fn sieve_of_eratosthenes(limit: usize) -> Vec {
    let mut is_prime = vec![true; limit + 1];
    let mut primes = Vec::new();
    for num in 2..=limit {
        if is_prime[num] {
            primes.push(Integer::from(num));
            for multiple in (num..=limit).step_by(num) {
                is_prime[multiple] = false;
            }
        }
    }
    primes
}

参考までに、100億以下の素数を列挙するのに要した時間は10分弱でした。

スレッド数を増やしたり、GPUによる並列処理を加えれば、実行速度はもっと早くなる可能性があります。それ以上に巨大な素数を列挙してどのような意味があるのかは未知数ですが‥。

素数を求めるRustプログラム (2025/7/8 更新)

たまたま暇だったので(受験生？)、時間と空間のトレードオフのうち「空間」を膨大にすることで、どうにか高速化しました。

具体的には、CUDAカーネルで区間篩を並列で実行して、それをRust側のzstdストリームに流してリアルタイム圧縮し、差分同士を抽出・記録することで、約4時間で1兆以下の素数を全て取得することができました。なお、整合性の検証はprimecountによって生成処理に別スレッドから追従する形で行っています。

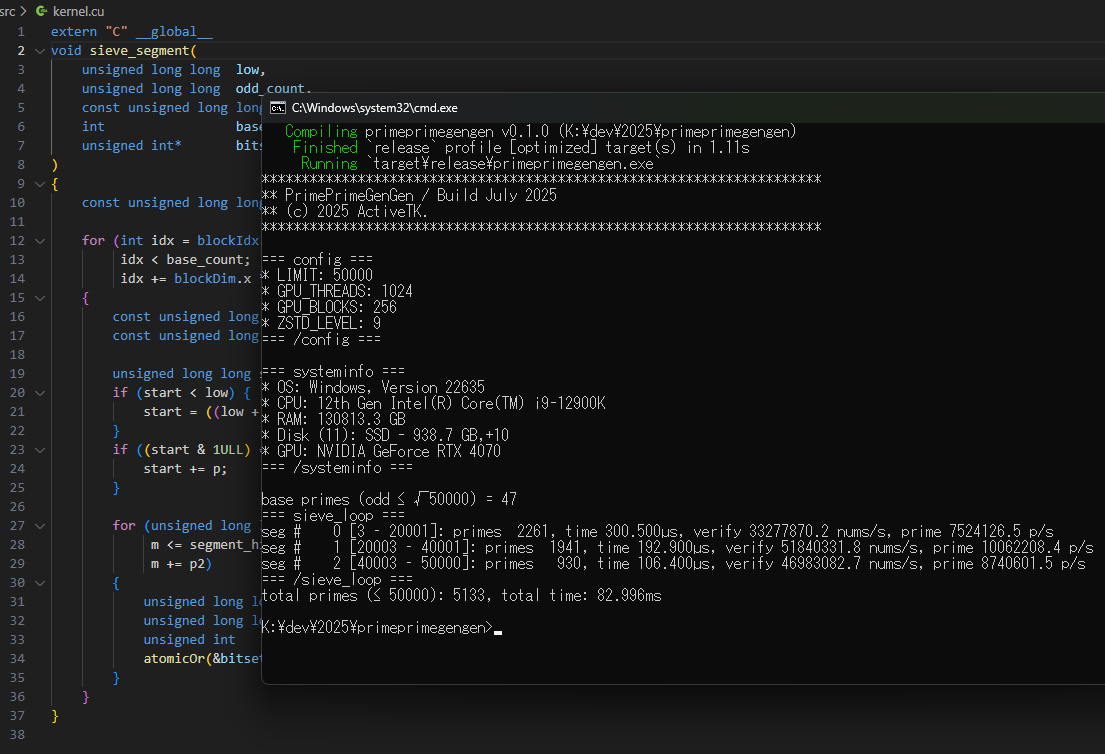
計算に使用したCUDAのコードは以下の通りです(kernel.cu)。

extern "C" __global__
void sieve_segment(
    unsigned long long  low,
    unsigned long long  odd_count,
    const unsigned long long* __restrict__ base_primes,
    int                 base_count,
    unsigned int*       bitset_words
)
{
    const unsigned long long segment_high = low + odd_count * 2ULL - 2ULL;
    const unsigned long long stride       = blockDim.x * gridDim.x;

    for (int idx = blockIdx.x * blockDim.x + threadIdx.x;
         idx < base_count;
         idx += stride)
    {
        const unsigned long long p  = base_primes[idx];
        const unsigned long long p2 = p * 2ULL;

        unsigned long long start;
        {
            unsigned long long rem = low % p;
            start = (rem == 0ULL) ? low : (low + (p - rem));
            if ((start & 1ULL) == 0ULL) start += p;
            if (start < p * p)        start = p * p;
        }
        if (start > segment_high) continue;

        for (unsigned long long m = start; m <= segment_high; m += p2) {
            unsigned long long offset = (m - low) >> 1ULL;
            unsigned int word = static_cast(offset >> 5ULL);
            unsigned int mask = 1U << (offset & 31ULL);
            atomicOr(&bitset_words[word], mask);
        }
    }
}

また、計算環境と所要時間は以下の通りです。

【systeminfo / results】
=== systeminfo ===
* OS: Windows, Version 22635
* CPU: 12th Gen Intel(R) Core(TM) i9-12900K
* RAM: 130813.3 MB
* Disk (11): SSD - 938.7 GB,+10
* GPU: NVIDIA GeForce RTX 4070
=== /systeminfo ===

total primes (≤ 10000000000): 455052511, total time: 172.136s
total primes (≤ 50000000000): 2119654578, total time: 1170.750s
total primes (≤ 100000000000): 4118054813, total time: 1531.126s
total primes (≤ 1000000000000): 37607912018, total time: 13818.578s

計算に使用したコード全体とログファイルは、こちらからダウンロードできます。

素数定理

素数の分布については、Prime Number Theorem（素数定理）があります。

具体的には、「π(x)」を「x以下の素数の個数」(素数計数関数)とするとき、xが十分大きい実数ならば、π(x)を(n/log n)で近似できます。

また、この定理より、素数が無限個あることが分かります。